このシリーズではE869120さんによって作成された競プロ典型90問をPythonで解いています。
問題
026 - Independent Set on a Tree(★4)
ポイント
隣り合わない頂点とは、辺で結ばれていない頂点を指します。
そのような頂点を選ぶには、深さが全て偶数、または奇数の頂点から選ぶと良いです。
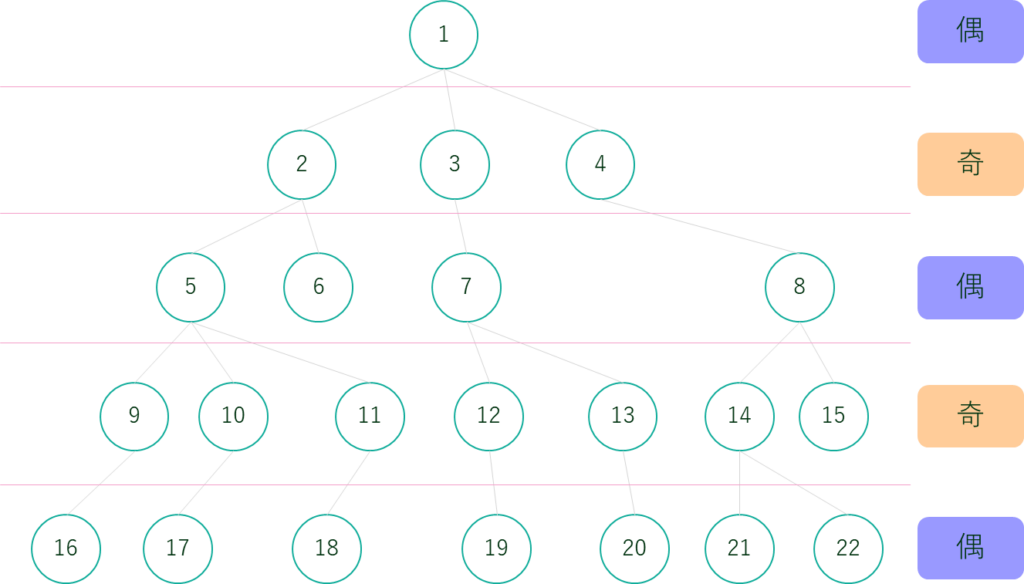
そのために
①各頂点の深さを調べる
②深さが偶数、奇数の頂点の数を比較して、多い方から2/N個選ぶ
といった手順で解いていきます。
以上を踏まえ、実装したコードがこちらです。
コード
def main():
import sys
from collections import deque
sys.setrecursionlimit(10 ** 9)
input = sys.stdin.readline
N = int(input())
# 木を作る
edge = [[] for _ in range(N+1)]
for _ in range(N-1):
a, b = map(int, input().split())
edge[a].append(b)
edge[b].append(a)
# 各頂点の深さのリスト 根の深さは0
depth = [N] * (N+1)
depth[1] = 0
# 深さが偶数・奇数の頂点のリスト
d_even = [1] # 根の深さ(=0)は偶数
d_odd = []
# 探索出発点の頂点をtodoに入れる。最初は根から
todo = deque()
todo.append(1)
# 各頂点の深さを求めていく。各頂点の深さは1つ上の頂点の深さ+1
while todo:
p_node = todo.popleft() # 出発点の頂点を取り出す
c_nodes = edge[p_node] # 出発点の1つ下の頂点達
for c in c_nodes:
if depth[c] != N: # 既に深さを確認した頂点ならば何もしない
continue
else:
depth[c] = depth[p_node] + 1 # 各頂点の深さは出発点の頂点の深さ+1
if depth[c] % 2 == 0: # 深さが偶数・奇数のリストにそれぞれ入れる
d_even.append(c)
else:
d_odd.append(c)
todo.append(c) # 次の出発点頂点としてcを入れる
# 深さが偶数・奇数の頂点のリストで長い方から2/N個取り出す
if len(d_even) >= len(d_odd):
print(*d_even[:N//2])
else:
print(*d_odd[:N//2])
if __name__ == '__main__':
main()