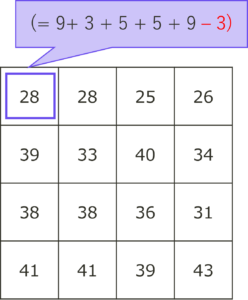
このシリーズではレッドコーダーが教える、競プロ・AtCoder上達のガイドライン【中級編:目指せ水色コーダー!】でまとめられている100問をPythonで解いています。
問題
AtCoder Regular Contest 054 B - ムーアの法則
ポイント
x年後のコンピュータでT(334)を解くのにかかる時間は
f(x) = x + P / 2 ^ (x/1.5)
と表すことができ、グラフは下記のような凸関数になります。(P=3.000の例)
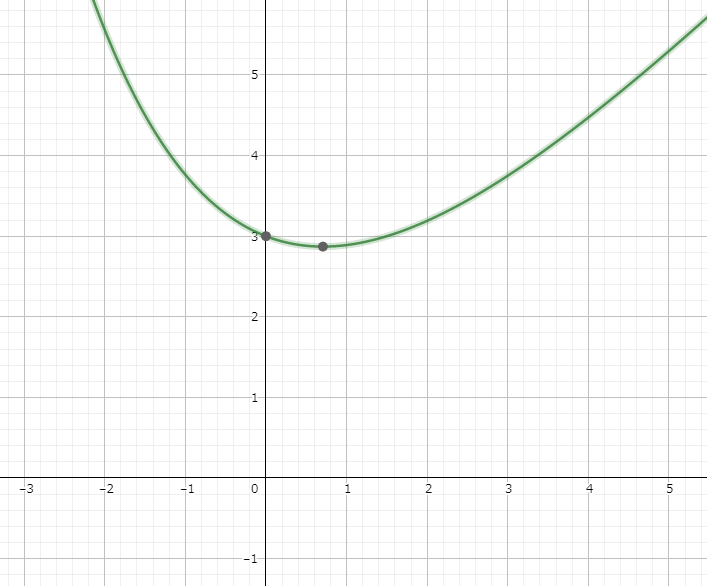
求めたい値はこのグラフで1番小さい値、すなわち頂点です。
頂点を求めるには三分探索という方法を使います。二分探索と基本的な考え方は同じです。
left, rightに対して三等分する点c1, c2を考えます。
上記グラフにおいて、
①f(c1) < f(c2)であれば、頂点はleftからc2の間に存在することがわかります。
②f(c1) > f(c2) であれば、 頂点はc1からrightの間に存在することがわかります。
このようにして徐々に探索の幅を狭めていきます。
(①の例ではc2を次のrightに、②の例ではc1を次のleftに設定します。 f(c1) = f(c2) の場合は①か②どちらか好きな方に含めてください。※<= または >= とする)
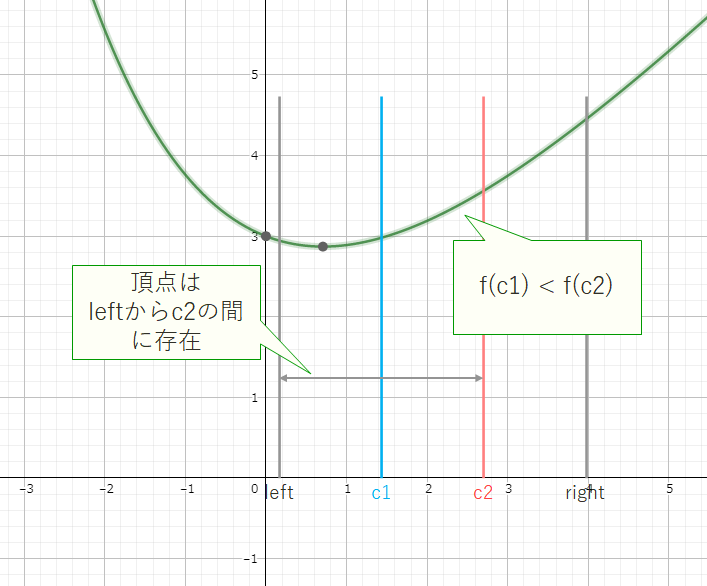
尚、三分探索では数式を直接解いて答えを導いている訳ではないので、得られる解はあくまで近似値となります。よって、三分探索を十分な回数(left-rightの幅の大きさが十分小さくなるまで)行うことによって解の精度を高めます。この問題においては誤差を10 ^ -8 以下に抑えます。
コード
def main():
import sys
sys.setrecursionlimit(10 ** 6)
input = sys.stdin.readline
P = float(input())
# 三分探索を行うための関数
def ternary_search(left: int, right: int):
while abs(left - right) > 1e-10: # leftとrightの差(探索の幅)が十分小さくなるまで行う
c1 = (2 * left + right) / 3
c2 = (left + 2 * right) / 3
if cal(c1) >= cal(c2):
left = c1
else:
right = c2
return (left + right) / 2 # 最終的にleftとrightの中間地点を頂点の近似解として返す
# x年後のコンピュータでT(334)を解くのにかかる時間を計算する関数
def cal(x: int):
return x + P / (2 ** (x / 1.5))
# 最初のleftの値は0(本問題ではx<0の場合は考えないので)、rightの値はleft-rightの範囲に頂点が含まれるように十分大きな値にする。
print(cal(ternary_search(0, 1000)))
if __name__ == '__main__':
main()