このシリーズではE869120さんによって作成された競プロ典型90問をPythonで解いています。
問題
ポイント
ある二次元配列Aを、ある二次元配列Bに一致させる方法があるかを探せば良いので、
単純にAの左上から値をBに合わせていって、最終的にAがBに一致するかを判断すればOKです。
この方法がAをBに一致させる最小の操作回数にもなります。
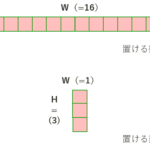
ここでポイントとなるのは、2種類の操作(1増やす or 1減らす)を行う際に選択できる範囲の
最小値は2x2の4マスであるということです。これはx=1, y=1を選択した場合です。

このため、Aの左上から順番に値を合わせていく際、ある制約が存在します。
それは、一番下の行(H行目)と一番右の列(W列目)の値をBに意図的に合わせることができないという点です。図で説明します。
以下のAをBに合わせる操作を考えます。
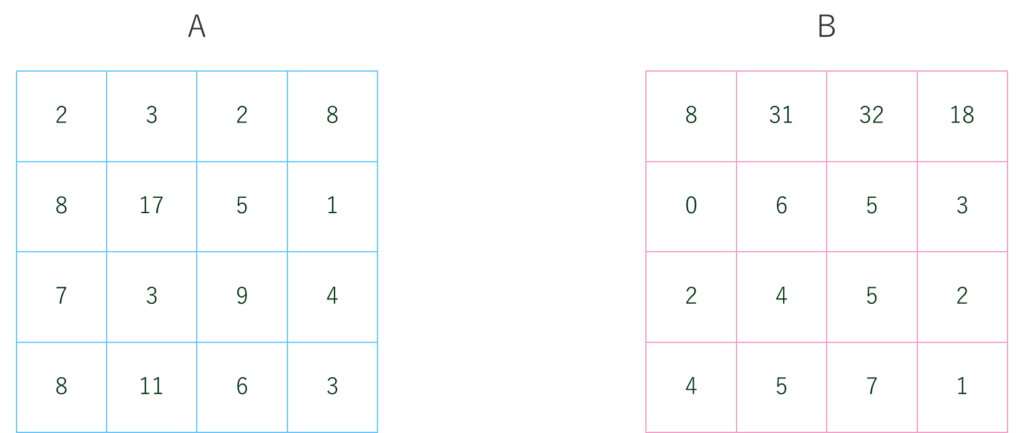
1回目の操作でAの左上2をBの左上8に合わせるため、周辺4マスを+6します。
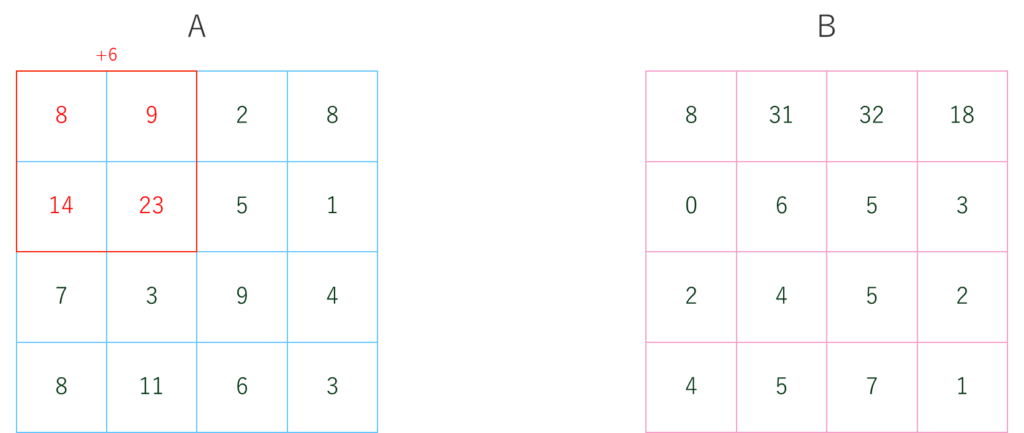
同様に、2,3回目の操作でAのマスをBのマスに合わせていきます。
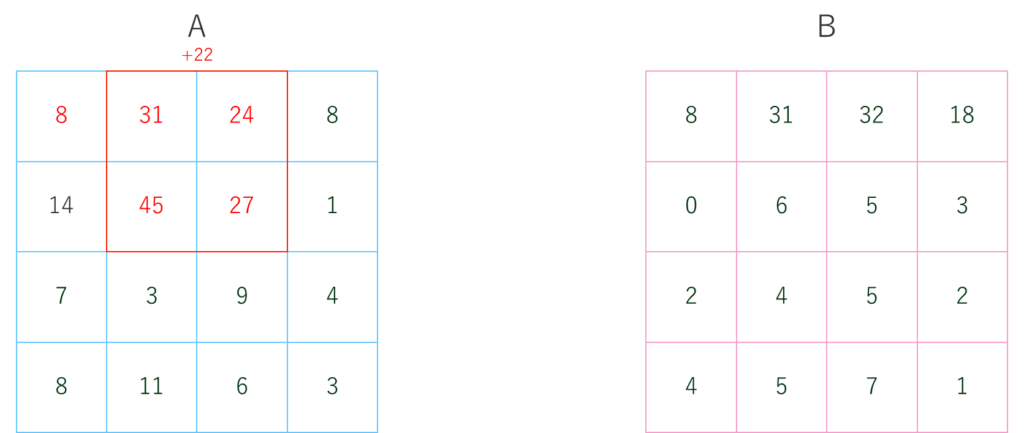
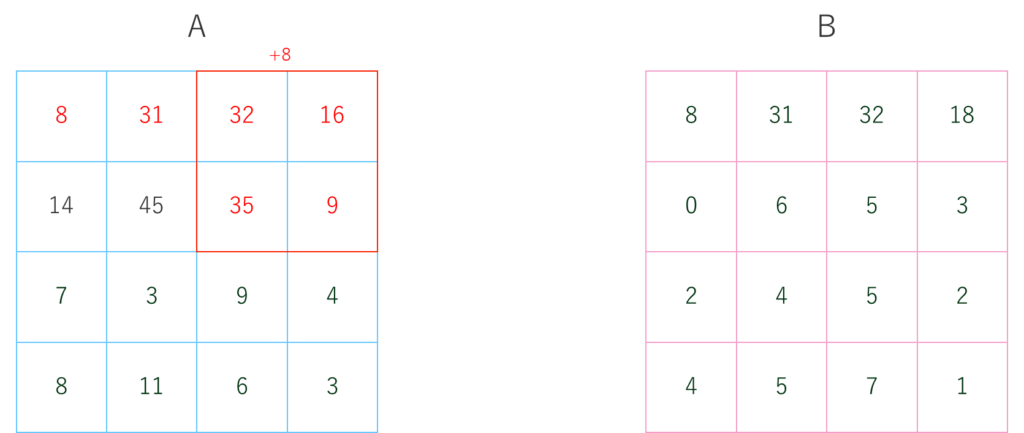
ここでAの右端のセル16について、Bのセル18に合わせるため操作を行うと、せっかく合わせた1つ手前のセル32がBと一致しなくなってしまいます。
このように、一番右の列のセルに関しては意図的にAをBに合わせることができません。
よって、以下の流れで回答を求めていきます。
①Aの左上からBの値に合わせていく。※一番右の列と一番下の行を除く。
②一番右の列と一番下の行に関してAとBの値が同じかを確認する。
③②で全てのセルが同じ値であれば、操作を0回以上行うことでAをBに一致させることは可能である。
以上を踏まえ、実装したコードがこちらです。
コード
def main():
import sys
sys.setrecursionlimit(10 ** 9)
input = sys.stdin.readline
H, W = map(int, input().split(" "))
A = [list(map(int, input().split(" "))) for _ in range(H)]
B = [list(map(int, input().split(" "))) for _ in range(H)]
# AをBに合わせる代わりに、AとBの差分の行列を作成→すべての要素を0にする操作を行っています。
# 特に理由はありません。気分です。
diff = [[A[h][w] - B[h][w] for w in range(W)] for h in range(H)]
cnt = 0 # 最小の操作回数
for h in range(H - 1):
for w in range(W - 1):
if diff[h][w] != 0:
value = diff[h][w]
# 操作を行う
diff[h][w] -= value
diff[h + 1][w] -= value
diff[h][w + 1] -= value
diff[h + 1][w + 1] -= value
cnt += abs(value)
else:
continue
# 一番右の列と一番下の行が0になっているか確認
for w in range(W):
if diff[H - 1][w] != 0:
print('No')
exit()
for h in range(H):
if diff[h][W - 1] != 0:
print('No')
exit()
print(f"Yes\n{cnt}")
if __name__ == '__main__':
main()