
このシリーズではE869120さんによって作成された競プロ典型90問をPythonで解いています。
問題
ポイント
この問題は累積和を使って解くとスムーズです。本問題に限らず、連続する~個のといった言葉が出てきたら累積和を使えないか考えてみるといいでしょう。
まず、N個のピースそれぞれの累積和を取ってみます。
N = 3 (1, 18, 1)の例

次に、それぞれのピースから連続するピースを選ぶ場合に条件を満たすような選び方があるかを
検討します。
例えば最初のピースの累積和は1ですが、もし
あるピースXの累積和 - 最初のピースの累積和 = ケーキ全体の10分の1 ※今回は2
となるピースが存在するのであれば最初のピースからあるピースXまでを選べば条件達成です。
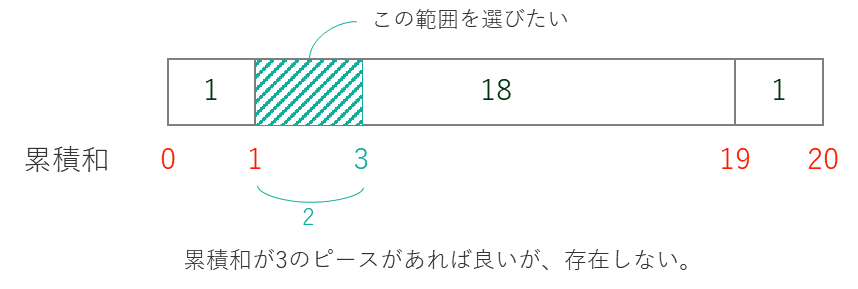
ここで、注意したい点がケーキは円形、すなわち1番目のピースとN番目のピースは繋がっているという点です。
上の例で3番目のピースを選んだ時、21の累積和のピースを選べば良いのですが存在しません。

しかし、実際のケーキは円形なのでこんな形をしており、3番目のピースと1番目のピースを
選べば条件達成です。
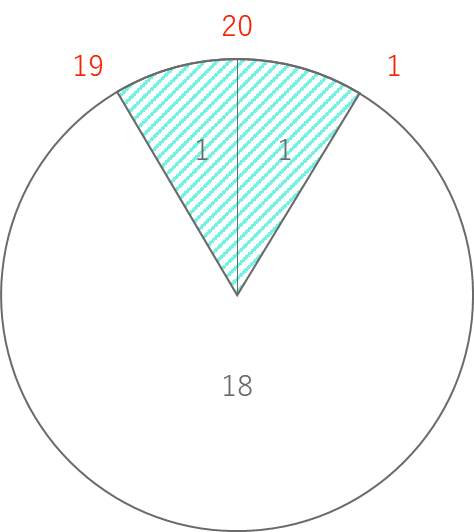
このような選び方を探索するには、各ピースの累積和を検討する際、累積和を全体の大きさ
(今回は20)で割ると上手くいきます。
先ほど3番目のピースを選んだ時に21の累積和のピースを探す例を出しましたが、
実際は累積和が1のピースを選ぶ事で条件が達成できました。
そして、21と1という数字には、全体の大きさ20で割った余りが同じ(=1)という共通点があります。
この性質を利用して、各ピースの選び方を全探索するのが今回のポイントです。
具体的には、各ピースをスタート地点として連続するピースの選び方を探索する際、
他のピースで累積和が
(スタートピースの大きさ + 全体の大きさ÷10) を全体の大きさで割った余り
のものがあるかを探索し、あれば条件に当てはまる選び方が存在します。
※超わかりにくいと思いますが、ぜひ一度紙に書いて考えてみてください。
語彙力がなくてスミマセン…。
以上を踏まえ、実装したコードがこちらです。
コード
def main():
import sys
sys.setrecursionlimit(10 ** 9)
input = sys.stdin.readline
N = int(input())
A = list(map(int,input().split(" ")))
# ケーキ全体の大きさが10の倍数でないならNo(自明)
if sum(A) % 10 != 0:
print('No')
exit()
# 累積和のリストを作成する
accum = [0]
for a in A:
accum.append(accum[-1] + a)
length = accum[-1] # ケーキ全体の大きさ
accum = set(accum) # in list よりもin setの方が計算量が少ないのでsetにする
# 条件に当てはまる累積和が存在するか調べる
for x in accum:
if (x + length // 10) % length in accum:
print('Yes')
exit()
print('No')
if __name__ == '__main__':
main()


