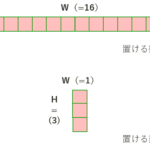
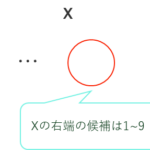
このシリーズではE869120さんによって作成された競プロ典型90問をPythonで解いています。
問題
ポイント
1回の魔法で各ボールは2つに分裂できるので、必要な操作の回数は元の整数xを因数分解した時の因数の数の対数、すなわちlog2(因数の数)の小数点以下切り上げで求めることができます。
図にするとこんなイメージです。(x = 48の場合)
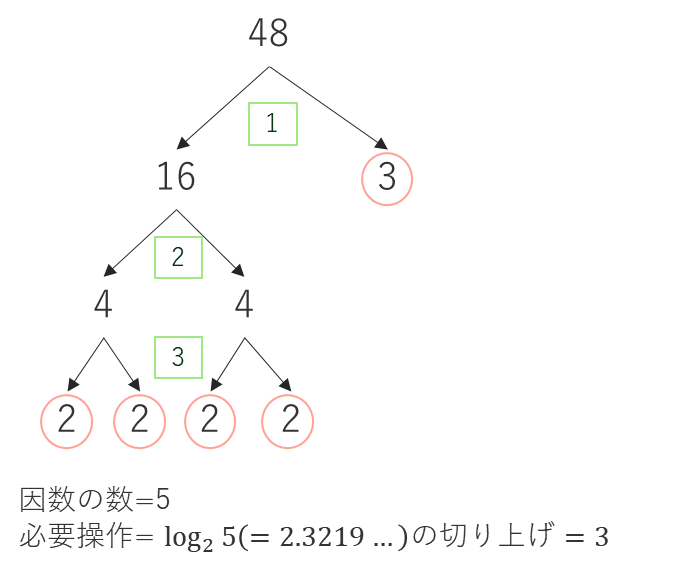
よって
①整数xを因数分解して因数の数を求める
②log2(因数の数)の小数点以下切り上げを求める
といった順序で解いていきます。
①の因数分解についてですが、ある数xを因数分解できるとき、xは2から√xまでの間に約数を必ず持ちます。(数学的証明は調べてみてください)
なのでプログラミングで因数分解をする時は2から√xまでの数でxを順番に割っていき、もし割り切れたらその商を更に同じ約数で割ることで達成できます。
ちょっとややこしいかもしれないので、ぜひデバッグしながらコードの流れを追ってみてください。
尚、√を求めるのはnumpy.sqrtを、小数点切り上げを求めるのはmath.ceilを使用すると便利です。
以上を踏まえ、実装したコードがこちらです。
コード
def main():
import sys
import numpy as np
import math
sys.setrecursionlimit(10 ** 9)
input = sys.stdin.readline
N = int(input())
# 因数分解して因数の数を求める
cnt = 0 # 因数の数
root = int(np.sqrt(N)) # 因数分解は2から√Nまでの数で
for i in range(2, root + 1):
while (N % i) == 0:
cnt += 1
N //= i
# 最後に残った因数が1以外のときは一番大きな因数となるので数にいれる
if N != 1:
cnt += 1
# log2cntの切り上げを求める
ans = math.ceil(np.log2(cnt))
print(ans)
if __name__ == '__main__':
main()