問題
ポイント
ボタンAを押した場合の処理は関数で用意するとして、愚直にK回その処理を行うとTLEとなってしまいます。
そこで、ボタンAの処理を何回か行った際、1度出てきた数字に戻ってきた場合を考えます。
図にするとこんな感じです。※青丸がボタンAを押した後の数字、ピンクがAを押した回数
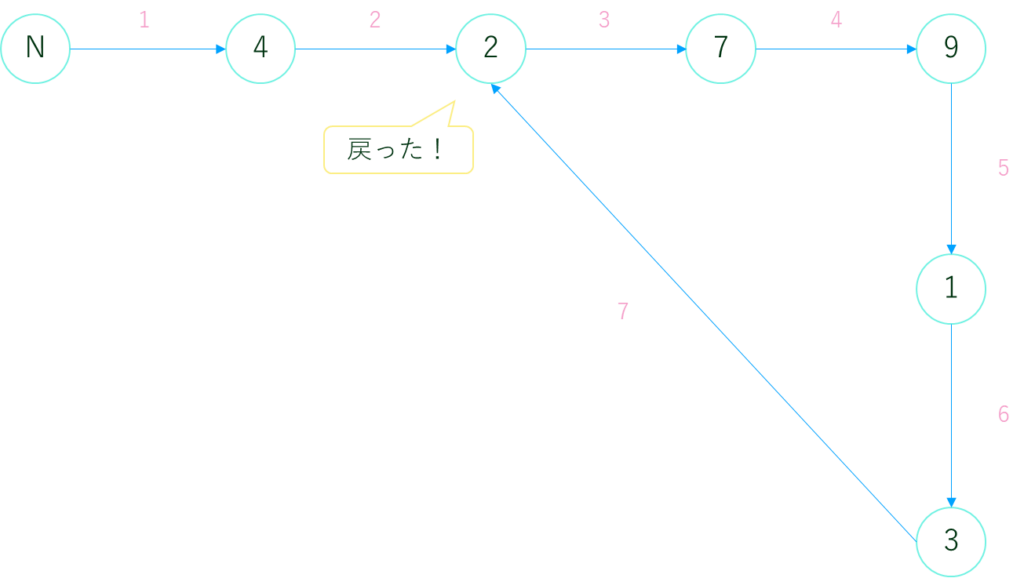
こうなった場合、その後何回ボタンAを押そうとも数字の遷移は2→7→9→1→3となります。
このことを利用して、実際にボタンAの処理を行う回数を減らしたいと思います。
具体的には、ボタンを押す回数Kを
K = (K - ループが起こるまでボタンを押す回数)÷ ループの大きさ + ループが起こるまでボタンを押す回数
に置き換えます。
上の例では
K = (K - 2)÷ 5 + 2 となります。
このようにすることで、実際にボタンAの処理を行う回数を減らし、TLEを回避します。
尚、ループが全く起こらない巨大なKが問題として与えられた場合はどうしようもないのですが、
そこは出題者側で調整されているのか、数学的にループが必ず起こることが証明できるのかは
私も分かっていません…。誰か教えてください。。
以上を踏まえ、実装したコードがこちらです。
コード
def main():
import sys
sys.setrecursionlimit(10 ** 9)
input = sys.stdin.readline
def A(x):
return (x + sum(map(int, list(str(x))))) % 100000
N, K = map(int, input().split())
done = [0] * (10**5)
cnt = 0 # ループが起こるまでボタンを押す回数
tmp = N
while True:
cnt += 1
tmp = A(tmp)
if done[tmp] != 0: # 同じ数字に戻ってきたらループの大きさを記録
loop_size = cnt - done[tmp]
break
else:
done[tmp] = cnt
# Kを置き換える
if K > cnt: # Kがcnt以下の場合はそもそもloopが発生しない
K = (K-cnt) % loop_size + cnt
for _ in range(K):
N = A(N)
print(N)
if __name__ == '__main__':
main()