このシリーズではE869120さんによって作成された競プロ典型90問をPythonで解いています。
問題
ポイント
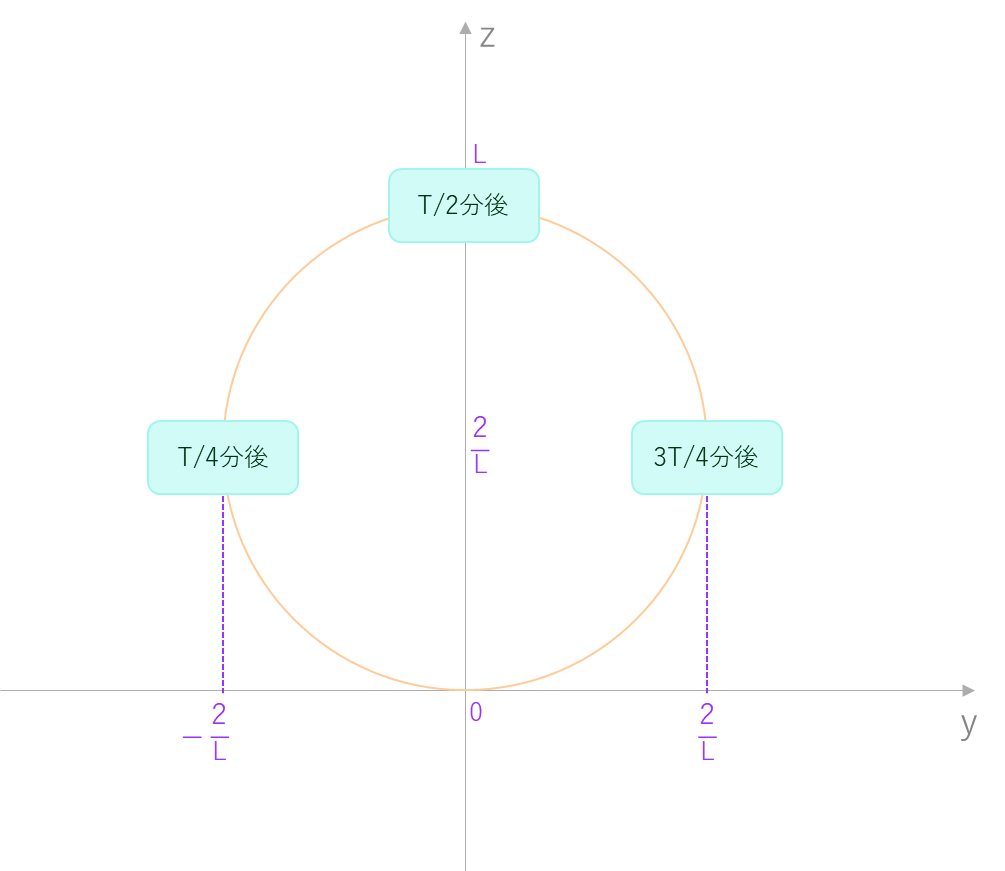
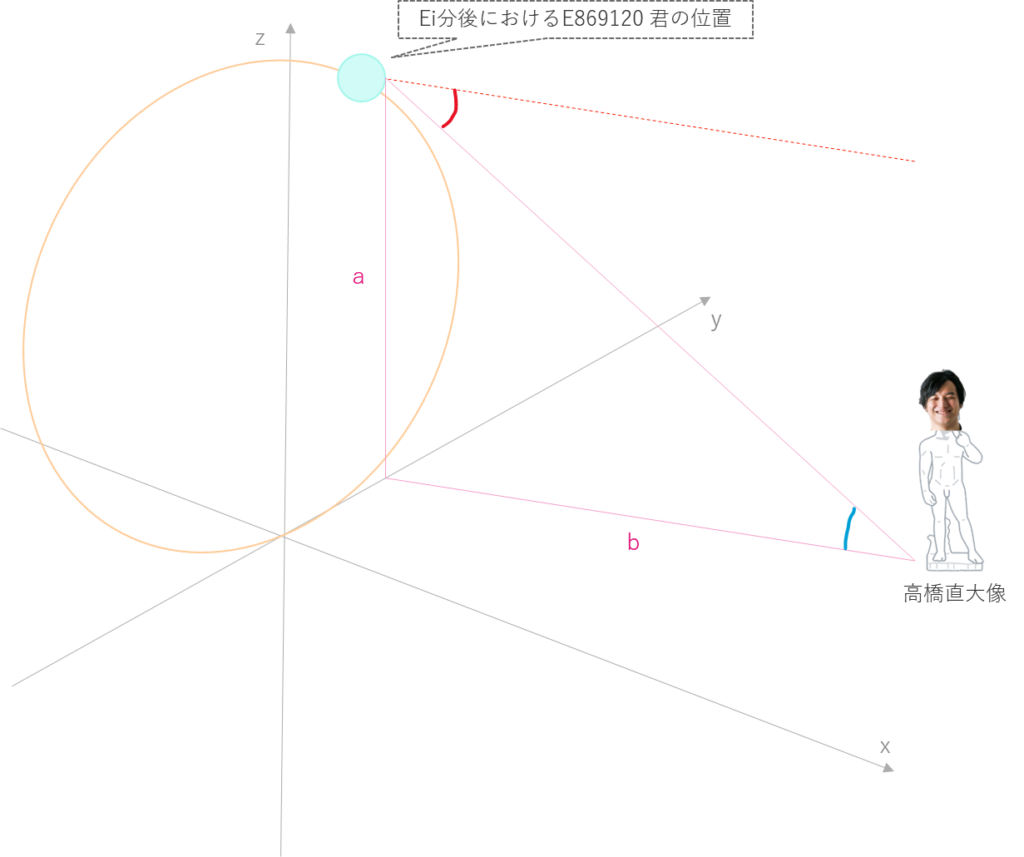
一旦問題の状況を図にしてみました。
観覧車ですが、平面 x=0 上にあるのでy軸とz軸だけ考えれば良さそうです。

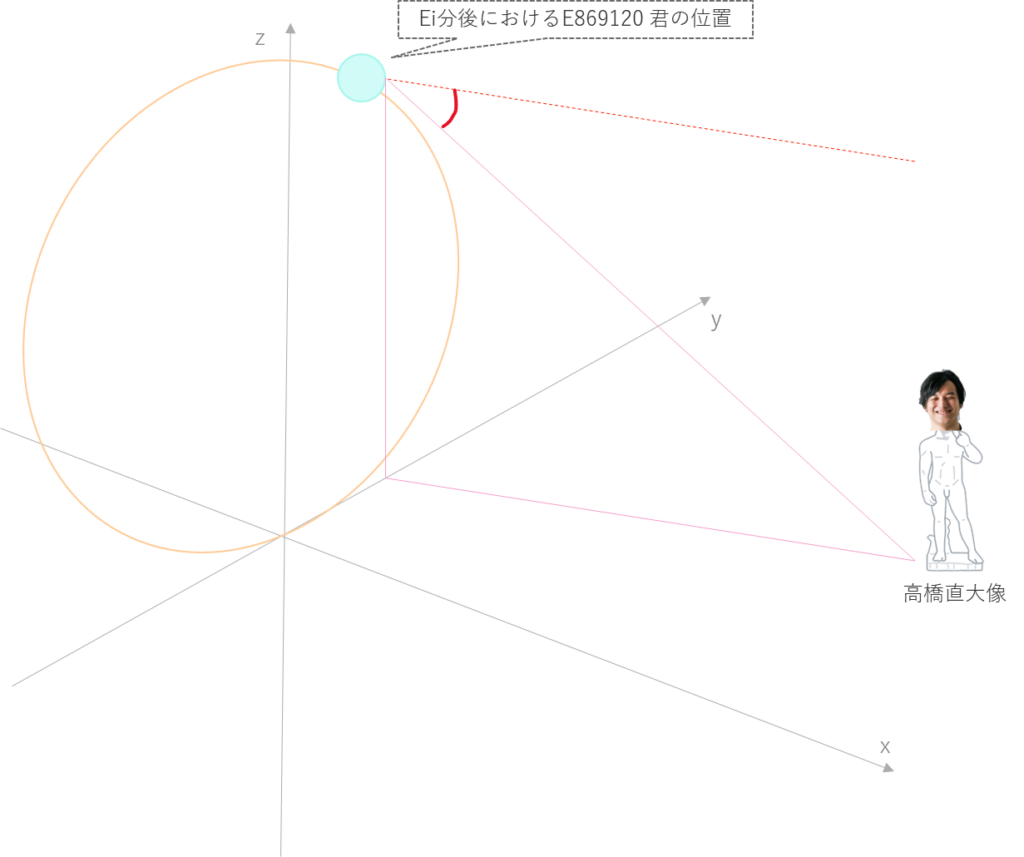
Ei分後の観覧車から見た高橋直大像の俯角は、図の赤の角度となります。
※ちなみに「俯角って何?」って方は以下の記事が参考になります。
高校数学ⅠA 三角比「相似からsin, cos, tan の意味を考える。仰角と俯角も」
ここで、平行線の錯覚の性質により、赤の角度と青の角度は同一となります。
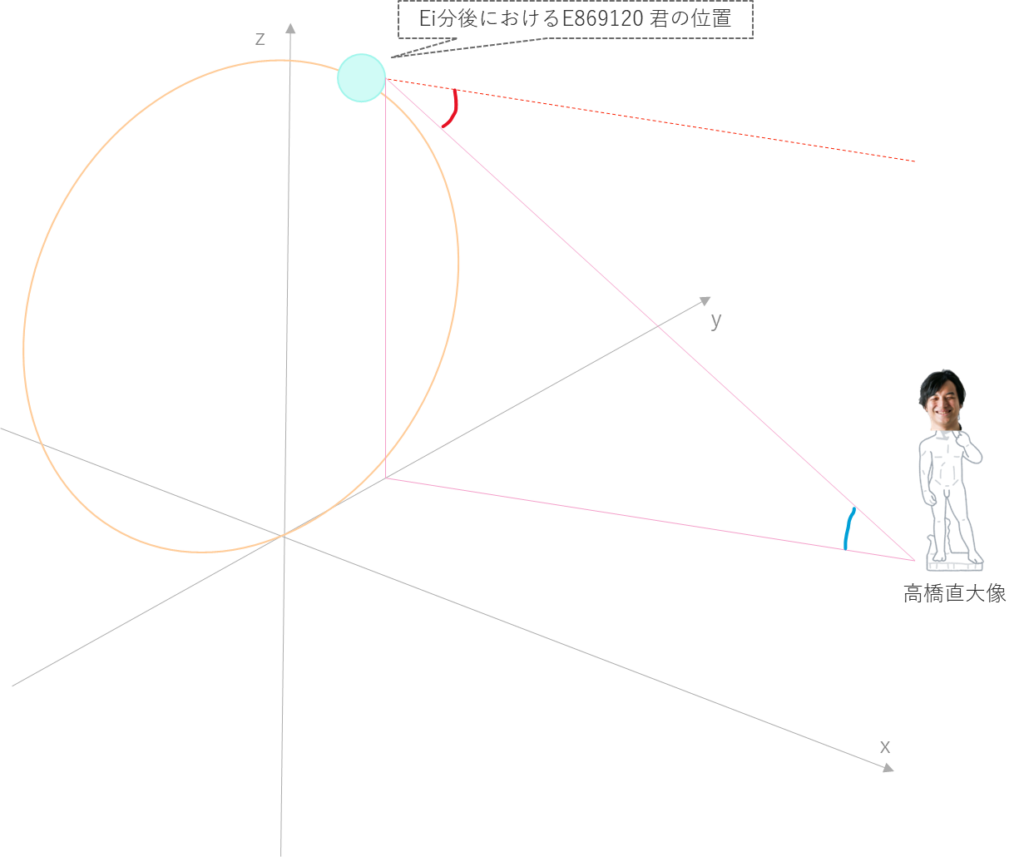
ピンクの三角形に注目すると、青の角度は辺a,bのアークタンジェントとなります。
※「アークタンジェントって何?」という方は下記記事がお役に立つかと!
たったの1分でわかる!アークタンジェントの基本【微分・積分】
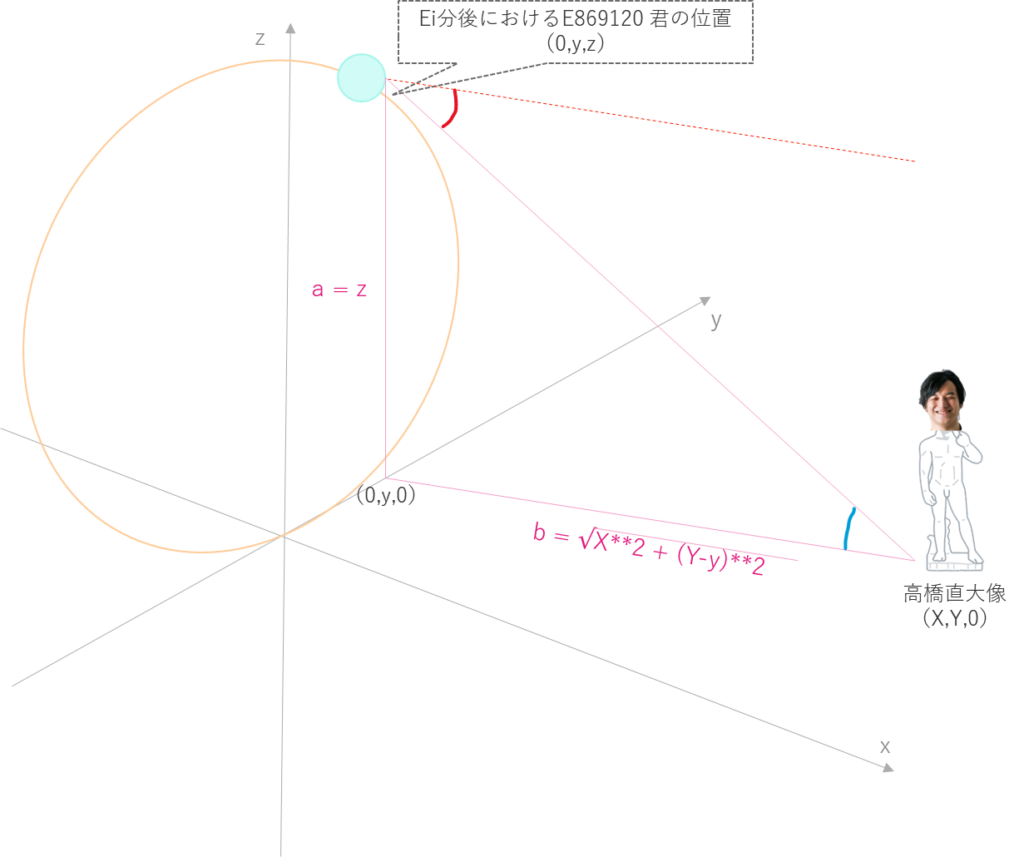
ここで、Ei分後におけるE869120 君の位置を(0,y,z)、高橋直大像の位置を (X,Y,0)とすると
辺a,bの長さは下記のように求めることができます。
ここまで大分長くなってしまいましたが…まとめると
・今回の問題は赤の角度を求めることがゴール
・赤の角度は青の角度と同じ
・青の角度を求めるために
①Ei分後におけるE869120 君の位置を求める
②辺a,bの長さを求める
③辺a,bのアークタンジェントを求める
といった手順で解いていきます。
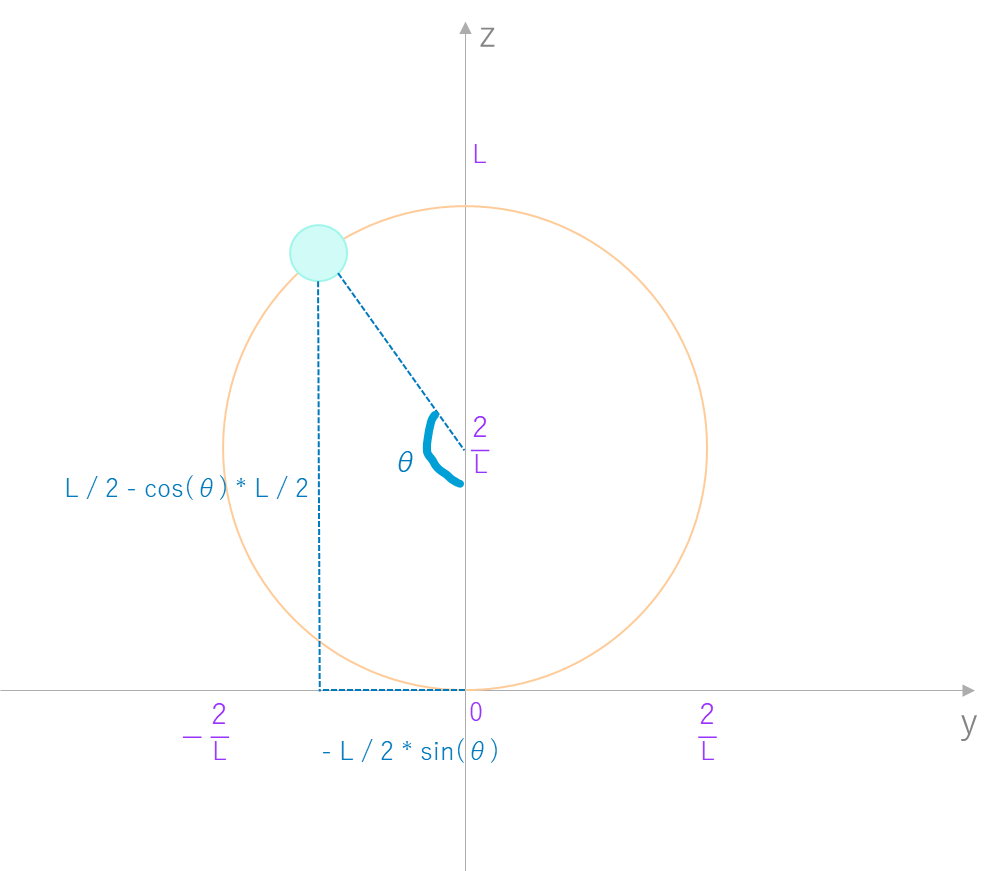
Ei分後におけるE869120 君の位置を求めるのも少し曲者なので補足しておきます。
Ei分後における観覧車の角度をθとすると、
E869120 君のx座標は 0(固定)
E869120 君のy座標は -L / 2 * sin(θ)
E869120 君のz座標は L / 2 - cos(θ) * L / 2
となります。
※三角関数に親しみが無い方だと、これを初見で理解するのは結構骨が折れる作業です。
単位円の三角関数について学んだ後、色々値を入れてみて実際に計算すると理解が早まると思います。
以上を踏まえ、実装したコードがこちらです。
コード
def main():
import sys
from math import pi, sin, cos, atan
sys.setrecursionlimit(10 ** 9)
input = sys.stdin.readline
T = int(input())
L, X, Y = map(int, input().split())
# Ei分後における、E869120君から見た高橋直大像の俯角を求める関数
def cal(e):
theta = e / T * 2 * pi # Ei分後の観覧車の回転角度
y = - L / 2 * sin(theta) # Ei分後のE869120君のy座標
z = L / 2 - cos(theta) * L / 2 # Ei分後のE869120君のz座標
b = (X ** 2 + (Y - y) ** 2) ** (1/2) # Ei分後の辺bの長さ
ans = atan(z / b) / pi * 180 # 辺aとbのアークタンジェント
return ans
Q = int(input())
for _ in range(Q):
E = int(input())
print(cal(E))
if __name__ == '__main__':
main()