このシリーズではE869120さんによって作成された競プロ典型90問をPythonで解いています。
問題
ポイント
この問題は動的計画法を使って解くとスムーズです。
動的計画法については下記記事の解説が分かりやすいと思います。
※いずれこのブログでも解説記事書きますのでお待ちを!
文字列Sのi文字目まで使用した時の、atcoderのj文字目までを完成させる方法が何通りあるかを
調べていき、最終的にSのN文字目まで使用した時にatcoderの7文字目(r)までを完成させる方法の通り数を出力します。
動的計画法の遷移は以下のイメージです。
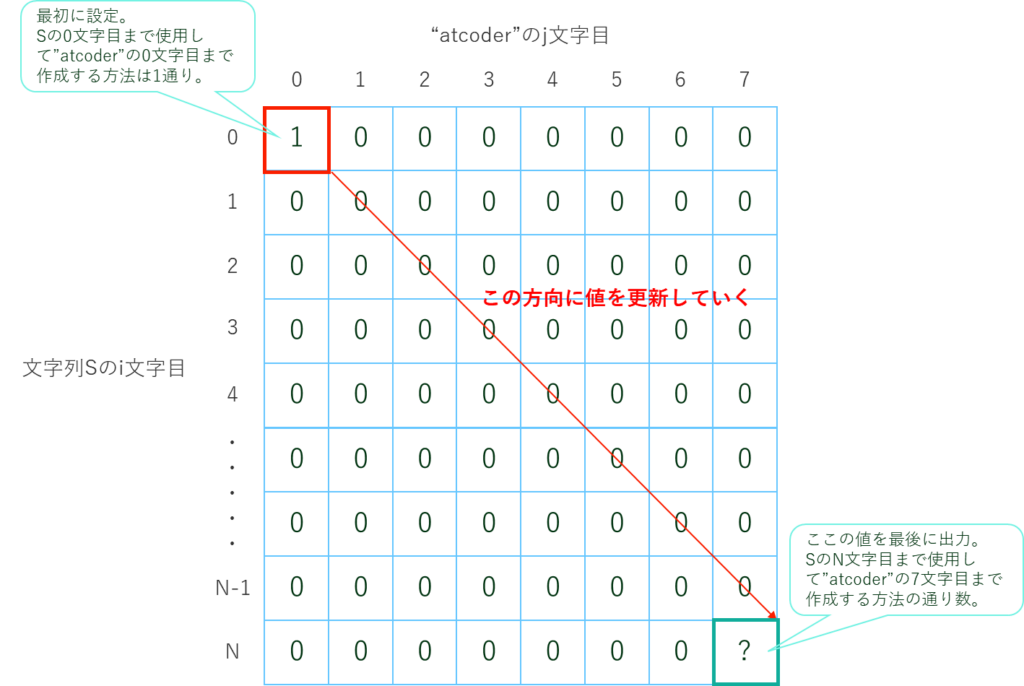
以上を踏まえ、実装したコードがこちらです。
コード
def main():
import sys
sys.setrecursionlimit(10 ** 9)
input = sys.stdin.readline
N = int(input())
S = input()[:-1]
MOD = 10 ** 9 + 7
# 作りたい文字列
T = 'atcoder'
len_T = len(T)
# dpの初期配列を準備
dp = [[0] * (len_T + 1) for _ in range(N+1)]
# 文字列Tの0文字目までを作る方法はそれぞれ1通り(取り出さない)
for i in range(N+1):
dp[i][0] = 1
# dpテーブルの更新 Sのi文字目とTのj文字目を比較している dpテーブルは0文字目から始めているので更新する際はiもjも+1する
for i in range(N):
for j in range(len_T):
if S[i] == T[j]:
dp[i+1][j+1] = dp[i][j] + dp[i][j+1]
dp[i+1][j+1] %= MOD
else:
dp[i+1][j+1] = dp[i][j+1]
dp[i+1][j+1] %= MOD
print(dp[N][len_T]%MOD)
if __name__ == '__main__':
main()